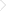前面有介绍过使用Gephi来建造传布图,图是Social Network剖析最常用的默示形式和体例,这篇文章介绍一下根基的相关常识。点击查看原始文档
Graph的相关根基概念
图(Graph):图是用来暗示一组物体之间的关系的体例。
节点(Node):节点是指要剖析的物体,每一个物体就是一个节点,好比在Social Network中每小我就是一个节点。
边(Edge):Graph中两个节点间的连线,用于暗示两个节点的关系。好比在Social Network中两小我的关注关系,微博传布骤瞰脾关系。
度(Degree):节点的度是指与其相连的边数,如不美观一个节点有3个边,那么这个节点的度就是3。
有向图(Directed Graph):边代表的关系具有标的目的的图。好比微博的关注关系,就是有标的目的的。
输入度(In-degree):有向图一一个节点收到的边。
输出度(Out-degree):有向图一一个节点发出的边。
无向图(Undirected Graph):边代表的关系没有标的目的的图。

Direct Graph
加权图(Weighted Graph):每个边权重分歧的图,边的权重可以代表相似度,距离或者链接成本等。加权图与有向和无向是两个分歧的维度。是以,在现实应用中会看到有向加权图(边既有标的目的又有权重)和无向加权图(边有权重但没有标的目的)。
Weighted Graph
属性图(Attributed Graphs):节点和边上可以承载更多的属性,这类图叫做属性图。

Attributed Graph
自我收集(Ego Networks):自我收集关注的不是收集整体而是以个体为中心,经由过程收集自我焦点联系关系的节点的信息,可觉得个体构建一个局部收集。
Ego Networks
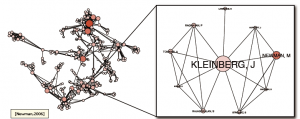
偶图(Bipartite Graphs):在偶图中节点被分成两个自力的集结,以确保统一集结中肆意两个节点都不共享一条边。
Actors-Movies Bipartite Graphs
多关系收集(Multi-Relational Networks):在良多社交收集剖析(SNA)的应用轨范中,在节得寄可能存在多种关系。在一种关系收集中节点间距离很近,而在另一种中则可能距离很远。
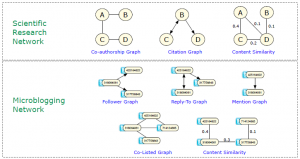
Multi-Relational Networks
路径(Path):图中年夜一个节获得另一个节点的一系列的边叫做路径。路径的长度就是边的个数,凡是是寻找两个节点间的最短路径。
图的直径:图的直径是指所有节点间的最短路径中的最长的那条。
连通图(Connected Graph):每个节点间都用路径连通的图。反之就长短连通图(Disconnected Graph)。
连通分支(Connected Component):如不美观一个连通图作为非连通图的一个成分,则这个连通图称为非连通图的连通分支。在良多现实的社交收集中,年夜部门节点将属于一个巨年夜的分支。
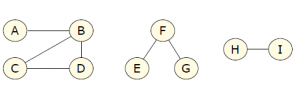
3 connected components
向心性的计较
临近节点(Neighbourhood):是指与它有边直接相连的节点(不搜罗它自身)。
集中系数(Clustering Coefficient):节点的集中系数=其临近的节点中有边相连的节点数/其临近节点总数。图的集中系数是其每个节点的聚类系数的平劫运。节点的集中系数默示了这个节点的临近节点的集中情形。图的集中系数剖明图的集中水平。
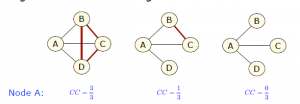
Clustering Coefficient
度中心性(Degree Centrality):计较一个节点的边数,度中心性关注单个节点。
Hub节点:度很高的节点。在收集中凡是饰演主要的脚色。对于一个有向的收集来说,输入度凡是用来代表受接待水平。
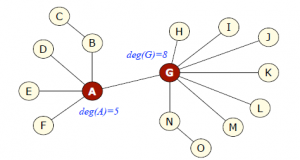
Degree
中介中心性(Betweenness Centrality):呈此刻良多其他节点间最短路径上的节点有较高的中介中心性分数。
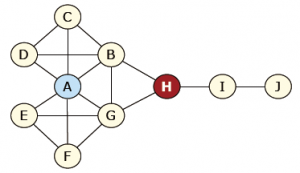
Betweeness Centrality
节点A的度中心性高于节点H,因为节点H的直接毗连更少。而节点H有更高的中介中心性,它在这个收集中饰演掮客人的脚色,它处在收集内良多节点交往的路径上,是以,它具有节制其他人交往的能力。
特征向量中心性(Eigenvector Centrality):一个节点的特征向量中心性与其临近节点的中心性得分的总和成正比。与主要的节点毗连的节点更主要。有少量有影响的联系人的节点其中心性可能跨越拥有年夜量平平的联系人的节点。这点与PR值近似。
特征向量中心性的计较:
1、计较图的核对临近矩阵的特征分化
2、选择有最年夜特征值的特征向量
3、第i个节点的中心性等于特征向量中的第i元素
注:相关网站培植技巧阅读请移步到建站教程频道。






 粤公网安备44010502000280号
粤公网安备44010502000280号 公众号二维码
公众号二维码
 小程序二维码
小程序二维码